CPLAnycubicPredator

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - CPL/Closed Polygon Lists
Introduced first in SolidGeometry 5.0, Creation date: 2020-12-31, Last change: 2025-08-18

Creates the CPL for the Anycubic Z-Level testing solid

Description

The original Anycubic Z-Level testing solid for the Predator/Delta-robot is available only as gcode

See Also: SGsample4APredator

Example Illustration

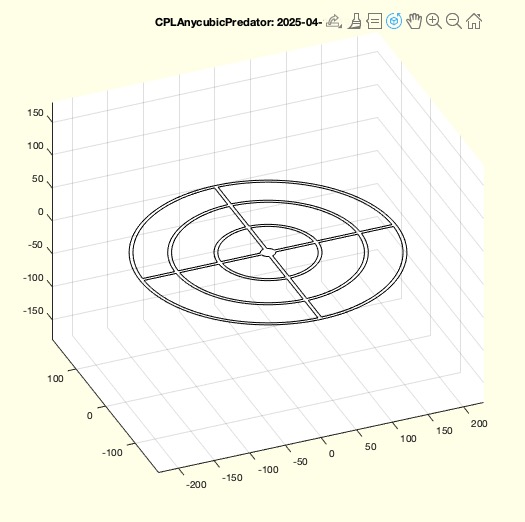
Syntax

CPL=CPLAnycubicPredator

Output Parameter

CPL: CPL of the contour of SGsample4APredator

Examples

Simply type
CPLAnycubicPredator

Copyright 2020-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This algorithm generates a Closed Polygon List (CPL) for the Anycubic Predator Z-Level testing solid. The function does not take any input parameters and outputs a CPL representing the contour of the testing solid.

Parameters and Variables

Do: An array [360, 260, 140, 20] representing diameters of circles.
Ro: An array calculated as half of each element in Do, representing radii of circles.
B: A constant value 5, used as a border or offset.
H: A constant value 1.5, not used in the algorithm.
CPL: An empty array initialized to store the final Closed Polygon List.

Algorithm Steps

Initialize the diameters array Do and calculate the radii Ro by dividing each element of Do by 2.
Initialize an empty array CPL to store the polygon data.
Iterate over each radius in Ro:

For each radius, append the circle polygon data generated by PLcircle(Ro(i)) to CPL.
Append a NaN separator to CPL.
Append the inner circle polygon data generated by PLcircle(Ro(i)-B) to CPL.
Append another NaN separator to CPL.

Remove the last NaN separator from CPL.
Union the current CPL with a square polygon generated by PLsquare(max(Do)-B/2, B).
Union the current CPL with another square polygon generated by PLsquare(B, max(Do)-B/2).
Union the current CPL with a circle polygon generated by PLcircle(min(Ro)).
If no output argument is specified, plot the CPL using SGfigure and CPLplot functions.

Algorithm explaination created using ChatGPT on 2025-08-18 23:56. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21