CVL2periodic
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - CVL/Closed Vertex Lists
Introduced first in SolidGeometry 4.4, Creation date: 2018-11-25, Last change: 2025-09-14
converts a perodic spatial contour into three periodic discrete fnct
Description
This is an auxiliary function for the analysis and synthesis of periodically repeating contours: number, length, angle.
The topic of decomposing an orbital contour into a periodic function is a problem very similar to the problem of correlating two curves. For this reason, it makes sense to take a closer look at the functions SGof2CPLzheurist, SGof2CPLs and PLcorrelate. It is possible to use the existing grid points of a coordinate axis:
a) simply map to an angular revolution
b) Map the total length of the contour to the angular revolution.
c) map the total sum of the angles of the contour to the angular revolution
In all three cases, additional interpolation values may have to be found to prepare the function for Fourier decomposition. Points may also need to be removed.
Another question is the "beginning" of the curve. If this is defined due to a maximum deflection of a value and if yes, which dimension is dominant or due to an angle relative to the center of the curve. It is about the discovery of the similarity of curves on the basis of initial criteria.
See Also: fourBarLinkage
, fourBarLinkageCPL
, SGof2CPLzheurist
, PLcorrelate
Example Illustration
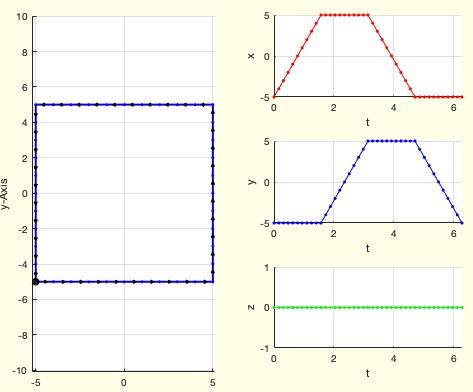
Syntax
[CPLx,CPLy,CPLz,t]=CVL2periodic(CVL,[tp])
Input Parameter
CVL: | | CPL or PL; only the first are used |
tp: | | time; default is 2* pi |
Output Parameter
CPLx: | | CPL [t x] |
CPLy: | | CPL [t y] |
CPLz: | | CPL [t z] |
t: | | time vector |
Examples
CVL2periodic(PLcircle(30))
CVL2periodic(PLcircle(30,6))
CVL2periodic(CPLaddauxpoints(PLcircle(30,6),1))
CVL2periodic(CPLaddauxpoints(PLsquare(10),1))
Copyright 2018-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Last html export of this page out of FM database by TL: 2025-09-21