ELsortFE
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - EL/Edge Lists
Introduced first in SolidGeometry 4.2, Creation date: 2018-04-18, Last change: 2025-09-14
groups and sorts unsorted edge lists
Description
Feature Edge lists are unsorted and not directed. This functions separates the edge lists into groups of meshes and contours and sorts contours into one direction. There is no guarantee that it is the right direction since the vertices are unknown to this function.
See Also: ELconnectedgroups
, CELofEL
Example Illustration
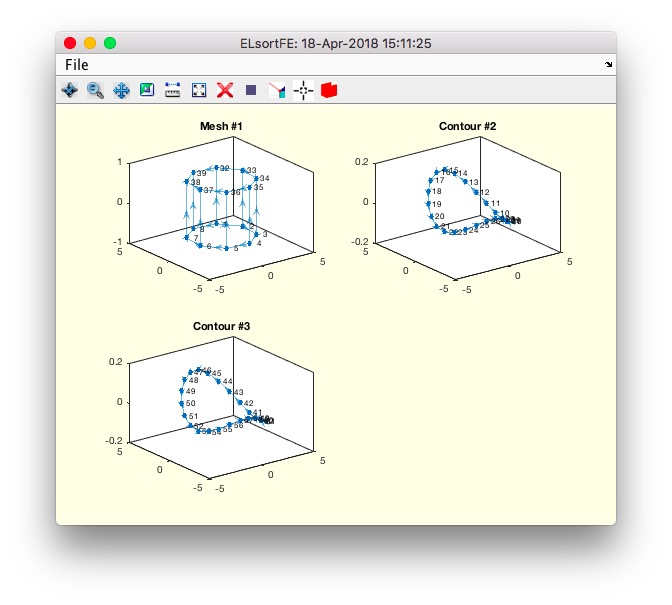
Syntax
[EL,CEL,mi]=ELsortFE(FEL)
Input Parameter
FEL: | | Unsorted edge list for instance a feature edge list |
Output Parameter
EL: | | Edge list |
CEL: | | Contour index list |
mi: | | mesh index; false = contour, true is mesh |
Examples
ELsortFE(FEofSG(SGsample(32)))
Copyright 2018-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This algorithm processes an unsorted edge list, typically a feature edge list, to group and sort the edges into meshes and contours. The contours are sorted in one direction, but the correct direction is not guaranteed due to unknown vertices.
Input Parameters
- FEL: Unsorted edge list, such as a feature edge list.
Output Results
- EL: Sorted edge list.
- CEL: Contour index list.
- mi: Mesh index;
false indicates a contour, true indicates a mesh.
Algorithm Steps
- Call
ELconnectedgroups(FEL) to obtain NEL (connected edge list) and CIL (contour index list).
- Determine the number of groups
n from the size of CIL.
- Initialize
mi as a logical array of size n with false values.
- Set
EL to FEL and CEL to CIL.
- Iterate over each group
i from 1 to n:
- Calculate
a as the number of unique elements in the segment of NEL defined by CIL(i,1) to CIL(i,2).
- Calculate
b as the difference between CIL(i,2) and CIL(i,1).
- If
b < a, call CELofEL on the segment of NEL to obtain ELi; otherwise, set ELi to the segment of NEL and set mi(i) to true.
- Update the segment of
EL from CIL(i,1) to CIL(i,2) with ELi.
- If no output arguments are specified, plot the results:
- Create a new figure with
SGfigure and set the title with SGtitle.
- Calculate
c as the ceiling of the square root of n.
- For each group
i, create a subplot and plot the segment of EL using ELplot.
- Set the title of each subplot to indicate whether it is a mesh or contour.
Algorithm explaination created using ChatGPT on 2025-08-19 07:42. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21