RLdelauxpoints
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 1.1, Creation date: 2013-08-07, Last change: 2025-09-14
deletes supporting points of an open 2D contour to generate staight lines
Description
This function works ONLY IN 2D! since only the z coordinate of the cross product is evaluated and used for the decision
See Also: RLaddauxpoints
, PLELaddauxpoints
Example Illustration
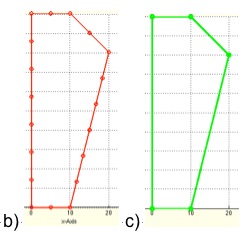
Syntax
[RL,i]=RLdelauxpoints(RL)
Input Parameter
Output Parameter
RL: | | Open 2D contour list |
i: | | index list of the original contour list |
Examples
Insert and delte auxiliary points into a simple contour
b=10; h=50; RL=[ 0 0;b 0;b h; 0 h];
RL=RLaddauxpoints (RL,8);
RL=RLdelauxpoints (RL,8);
Copyright 2013-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, RLdelauxpoints, is designed to process an open 2D contour list by removing auxiliary points to create straight lines. It is specifically tailored for 2D operations, as it only evaluates the z-coordinate of the cross product for decision-making.
Input Parameters
- RL: An open 2D contour list, represented as a matrix where each row corresponds to a point in 2D space.
Output Results
- RL: The modified open 2D contour list with auxiliary points removed.
- i: An index list indicating the positions of the original contour points that are retained in the modified list.
Algorithm Steps
- Check if the first and last points in the contour list
RL are identical. If they are, remove the last point to ensure the contour is open.
- Set a threshold value
thr to 1e-12 for decision-making purposes.
- Calculate backward vectors
AV by subtracting each point from the previous point in the list. For the first point, subtract it from the last point.
- Calculate forward vectors
BV by subtracting each point from the next point in the list. For the last point, subtract it from the first point.
- Compute the cross product of
AV and BV for each point, focusing on the z-component. This is done using the formula: AV(:,1) * BV(:,2) - AV(:,2) * BV(:,1).
- Determine which points are real corners by checking if the absolute value of the cross product is greater than the threshold
thr.
- Update the contour list
RL to include only the points identified as real corners.
Algorithm explaination created using ChatGPT on 2025-08-19 00:58. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21