SGdummyRjoint

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Modeling function
Introduced first in SolidGeometry 5.0, Creation date: 2020-10-04, Last change: 2025-09-14

creates a simple geometry to better imagine a rotating joint

Description

For w==0, frame C corresponds to eye(4) or T

See Also: SGdesignDIN912DIN985

Example Illustration

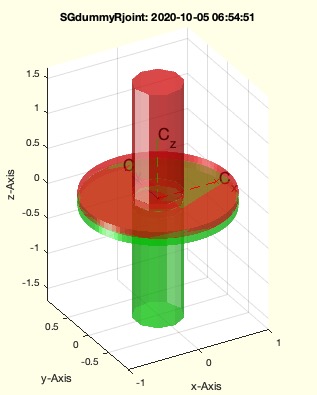
Syntax

SG=SGdummyRjoint([R,H,w,T])

Input Parameter

`R`:		[Ro Ri]
`H`:		[Hi Ho]
`w`:		rotation angle; default is 0
`T`:		Transformation matrix; default is eye(4)

Output Parameter

SG: SOlid Geometry of a dummy revolute joint

Examples


SGdummyRjoint

Copyright 2020-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, SGdummyRjoint, creates a simple geometry to visualize a rotating joint. It is part of the SolidGeometry library and was introduced in version 5.0. The function takes several input parameters and returns a solid geometry object.

Input Parameters

R: A vector [Ro Ri] representing the outer and inner radii. If only one value is provided, the inner radius is set to one-third of the outer radius.
H: A vector [Hi Ho] representing the heights. If only one value is provided, the outer height is set to one-tenth of the inner height.
w: The rotation angle, which defaults to 0. This parameter is not currently used in the function.
T: A transformation matrix, which defaults to the identity matrix eye(4).

Output

SG: The solid geometry of a dummy revolute joint.

Algorithm Steps

Retrieve the input parameters using getfuncparams. If the number of elements in R or H is 1, set default values for the missing elements.
Create a solid geometry SGA using SGofCPLz with a circle of radius R(2) and height H(1).
Create another solid geometry SG2 using SGofCPLz with a circle of radius R(1) and height H(2). Align SG2 to the bottom of SGA using SGtransrelSG.
Color the faces of SGA red and SG2 green using SGcolorfaces.
Combine SGA and SG2 into a cell array.
Create a mirrored version SGB of SGA by rotating it 180 degrees around the y-axis using SGtransrelSG and color its faces green.
Combine SGA and SGB into a cell array and convert it into a single solid geometry using SGofSG.
Retain specific fields ('VL', 'FL', 'FC') in the solid geometry using retainfields.
Set the transformation matrix of the solid geometry to the identity matrix using SGTset. If a transformation matrix T is provided, apply it using SGtransT.
If no output is requested, plot the solid geometry using SGfigure and SGTplotalpha with a transparency of 0.5.

Algorithm explaination created using ChatGPT on 2025-08-19 07:30. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21