SGinsertJoint

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Surfaces
Introduced first in SolidGeometry 4.1, Creation date: 2017-08-13, Last change: 2025-09-14

creates joint structures inside of a solid geometry

See Also:

Example Illustration

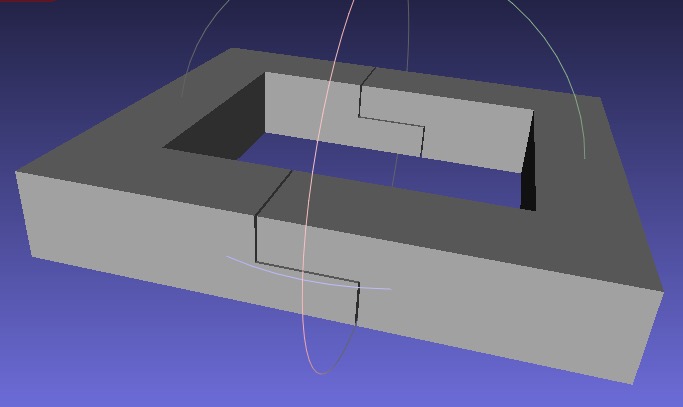
missing image of SGinsertJoint(SG,T,typ,x)

Syntax

SGR=SGinsertJoint(SG,T,typ,x)

Input Parameter

`SG`:		Solid Geometry
`T`:		Frame for the Solid Geometry
`typ`:		Type of joint
`x`:		parameter set

Output Parameter

SGR:

Examples


 SG=SGsample(29); SGinsertJoint(SG,TofR(rot(0,0,0),[0 +20 5]));

Copyright 2017-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, SGinsertJoint, is designed to create joint structures within a solid geometry. Below is a detailed explanation of the algorithm and its parameters.

Input Parameters

SG: Represents the solid geometry to which the joint will be added.
T: A transformation frame for the solid geometry, which defines the position and orientation.
typ: Specifies the type of joint to be created. In the provided code, it is set to 'cut'.
x: A parameter that influences the size or shape of the joint. In the example, it is set to 10.

Algorithm Steps

Initialize the solid geometry SG using SGsample(29).
Define the transformation T using TofR with a rotation and translation vector.
Set the slot width to 0.3 and overlap olap to 0.1.
Calculate crosspoints using crosspointsVLFLofT to determine the intersection of the geometry with the transformation frame.
Display the initial geometry using SGfigure.
Create a polygon line PL based on the parameter x and the depth d.
Grow the polygon line using PLgrowline with the slot width.
Generate a solid geometry A from the grown polygon line using SGofCPLz.
Rotate and translate A to align with the transformation T.
Create a second geometry B by translating A further along the y-axis.
Display the geometry A using SGfigure.
Retesselate both geometries A and B to a minimum area using SGretesselateAmin.
Perform boolean subtraction of A and B from the original geometry SG using SGbool.
Assign the result to SGR.
If no output is requested, plot the resulting geometry SGR using SGplot and set the lighting with setplotlight.

Algorithm explaination created using ChatGPT on 2025-08-19 00:57. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21