SGvenacavainferiorring
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Surfaces
Introduced first in SolidGeometry 4.8, Creation date: 2019-10-09, Last change: 2025-09-14
creates a ring for the Vena Carva Inferior
Description
At the request of Professor Dr. Peter Ewert, German Heart Center Munich
See Also: , SGspring
, SGstent
Example Illustration
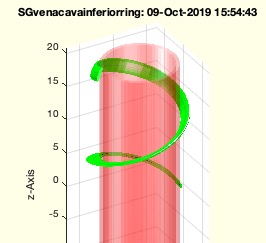
Syntax
[SGr,SGvci]=SGvenacavainferiorring([DA,dmin,dmax])
Input Parameter
DA: | | Diameter of the Carva Inferior vein |
dmin: | | minimal diameter of the ring |
dmax: | | maximal diameter of the ring |
Output Parameter
SGr: | | Solid of Ring to placed through catheter |
SGvci: | | Solid Geometry of Carva Inferior vein |
Examples
SGvenacavainferiorring(12,1,2)
Copyright 2019-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This algorithm is designed to create a ring for the Vena Cava Inferior, a large vein in the human body. The function is part of the SolidGeometry library and is used to model the geometry of the vein and the ring that can be placed through a catheter.
Input Parameters
- DA: Diameter of the Vena Cava Inferior vein. Default value is 12 mm if not provided.
- dmin: Minimal diameter of the ring. Default value is 1 mm if not provided.
- dmax: Maximal diameter of the ring. Default value is equal to
dmin if not provided.
Output Results
- SGr: Solid of the ring to be placed through a catheter.
- SGvci: Solid Geometry of the Vena Cava Inferior vein.
Algorithm Steps
- Calculate the radius of the Vena Cava Inferior vein as
RA = DA / 2.
- Create a cross-sectional profile
CPLv for the vein using two circles with radii RA - dmax/2 - 0.5 and RA - dmax/2 - 1, separated by a NaN value to indicate a break.
- Generate the solid geometry
SGvci of the vein using SGofCPLz with 40 segments, and translate it by [0 0 -20] mm.
- Create a helical path
CVL with radius RA, height 20 mm, and 3Ã turns using VLhelix.
- Define a circular cross-section
CPL for the ring with a minimum diameter dmin/2 and a maximum diameter dmax/2.
- Generate the solid geometry
SGr of the ring using SGcontourtube2 with the cross-section CPL and the helical path CVL.
- If no output arguments are specified, visualize the results:
- Open a new figure with
SGfigure and set the view to [-30, 30] degrees.
- Plot the vein geometry
SGvci in red with 20% transparency using SGplotalpha.
- Plot the helical path
CVL in blue using CVLplot.
- Plot the ring geometry
SGr in green with 90% transparency using SGplotalpha.
Algorithm explaination created using ChatGPT on 2025-08-19 07:06. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21