TR3ofVM

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - VM/Voxels
Introduced first in SolidGeometry 2.1, Creation date: 2015-01-20, Last change: 2025-08-19

returns a

Example Illustration

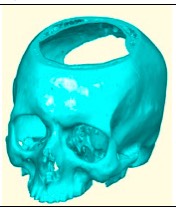
Syntax

[TR4,TR3]=TR3ofVM(V,[vs,s])

Input Parameter

`V`:
`vs`:
`s`:

Output Parameter

`TR4`:
`TR3`:

Copyright 2015-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, TR3ofVM, is designed to process a 3D voxel matrix and generate triangulations. Below is a detailed explanation of the algorithm and its parameters.

Input Parameters

V: A 3D matrix representing voxel data.
vs: An optional parameter specifying voxel scaling factors. Default is [1, 1, 1].
s: An optional scaling factor for voxel resolution. Default is 1.

Output Results

TR4: A 4D triangulation object.
TR3: A 3D triangulation object representing the surface.

Algorithm Steps

Initialize voxel scaling factors vs to [1, 1, 1]. If provided, update vs with the first optional argument.
Initialize scaling factor s to 1. If provided, update s with the second optional argument and adjust vs accordingly.
Downsample the voxel matrix V using the scaling factor s.
Compute the vertex list VL from the downsampled voxel matrix using the function VLofVM.
Create a 4D Delaunay triangulation TR4 from the vertex list VL.
Extract the points and connectivity list from TR4.
Initialize an array isInterior to mark interior tetrahedra.
Iterate over each tetrahedron in the connectivity list:

Extract the vertices of the tetrahedron.
Calculate the pairwise distances between vertices.
Mark the tetrahedron as non-interior if any distance exceeds 4 units.

Convert isInterior to a logical array.
Scale the vertex list VL by the voxel scaling factors vs.
Select the vertices and tetrahedra that are marked as interior using VLELselect.
Create a new triangulation TR4 with the selected vertices and tetrahedra.
Extract the free boundary (surface) of the triangulation TR4 to form FL.
Select the vertices and faces of the free boundary using VLELselect.
Create a 3D triangulation TR3 from the free boundary.
If no output arguments are specified, visualize the surface using VLFLfigure and VLFLplots.

Algorithm explaination created using ChatGPT on 2025-08-19 00:40. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21