VLFLarea
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Geometric Queries
Introduced first in SolidGeometry 2.8, Creation date: 2016-01-10, Last change: 2025-09-14
returns the area of the surfaces (VL/PL)
Description
With respect to Heron: A=sqrt(s(s-a)(s-b)(S-c)); s=0.5*(a+b+c).
This function support point lists (2D) or vertex lists (3D)
See Also: SGarea
, CPLarea
Example Illustration
Syntax
[ASUM,A]=VLFLarea(VL,FL,[fil])
Input Parameter
VL: | | Vertex list (nx3) or Point List (nx2) |
FL: | | Facet list |
fil: | | optional list of facet; default is 1:size(FL,1) |
Output Parameter
ASUM: | | Area of the surfaces |
A: | | Area list for facet list |
Examples
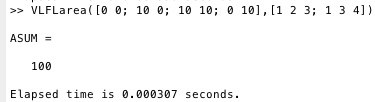
Try:
VLFLarea([0 0; 10 0; 10 10; 0 10],[1 2 3; 1 3 4])
Copyright 2016-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function calculates the area of surfaces defined by vertex and facet lists using Heron's formula. It supports both 2D point lists and 3D vertex lists.
Input Parameters
- VL: Vertex list (nx3) or Point List (nx2). It contains the coordinates of the vertices.
- FL: Facet list. It defines the connectivity of the vertices to form facets (triangles).
- fil: Optional list of facets to consider. Default is all facets (1:size(FL,1)).
Output Results
- ASUM: Total area of the surfaces.
- A: List of areas for each facet.
Algorithm Steps
- Initialize
fil to include all facets if not provided.
- Determine the number of facets to process (
nf).
- Initialize an area list
A with zeros.
- If no output is expected, start a timer.
- For each facet in
fil:
- Calculate the lengths of the sides
a, b, and c using the Euclidean norm.
- Compute the semi-perimeter
s as 0.5 * (a + b + c).
- Calculate the area of the facet using Heron's formula:
A(i) = sqrt(s * (s-a) * (s-b) * (s-c)).
- Sum the areas of all facets to get
ASUM.
- If no output is expected:
- Display the total area
ASUM.
- Plot the facets using
SGfigure and VLFLplot functions.
Algorithm explaination created using ChatGPT on 2025-08-18 07:37. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21