VLFLofBB

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Modeling function
Introduced first in SolidGeometry 1.1, Creation date: 2013-07-17, Last change: 2025-09-14

return VL and FL for solid related to a bounding box

Description

This function is described in chapter 2 of the article collection of Tim Lueth and Franz Irlinger on the automatic construction of 3D printable mechanisms

See Also: , BBofVL , CPLofBB , SGofBB , BBofSG

Example Illustration

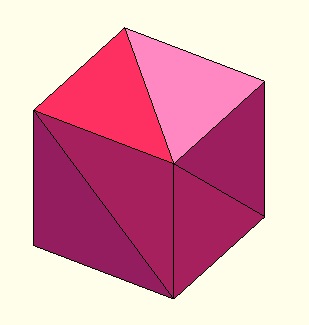
Syntax

[VL,FL]=VLFLofBB(BB)

Input Parameter

BB: Bounding box [xmin xmax ymin ymax zmin zmax]

Output Parameter

`VL`:		Vertex list
`FL`:		Facet list

Examples


VLFLofBB([0 10 0 10 0 10])

Copyright 2013-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, VLFLofBB, is designed to generate a vertex list (VL) and a facet list (FL) for a solid object defined by a bounding box (BB). The function is part of the SolidGeometry library and was introduced in version 1.1.

Input Parameters

BB: A bounding box defined by six parameters: [xmin, xmax, ymin, ymax, zmin, zmax]. These parameters specify the minimum and maximum extents of the box along the x, y, and z axes.

Output Results

VL: The vertex list, which contains the coordinates of the vertices of the bounding box.
FL: The facet list, which describes the faces of the convex hull of the bounding box.

Algorithm Steps

The function begins by defining the vertices of the bounding box using the input parameters. The vertices are defined in a 3D space as follows:
- Vertex 1: (xmin, ymin, zmin)
- Vertex 2: (xmax, ymin, zmin)
- Vertex 3: (xmax, ymax, zmin)
- Vertex 4: (xmin, ymax, zmin)
- Vertex 5: (xmin, ymin, zmax)
- Vertex 6: (xmax, ymin, zmax)
- Vertex 7: (xmax, ymax, zmax)
- Vertex 8: (xmin, ymax, zmax)
A Delaunay triangulation is performed on the vertex list using the DelaunayTri function. This step creates a tessellation of the 3D space defined by the vertices.
The convex hull of the tessellated space is computed using the convexHull function. The convex hull represents the smallest convex shape that encloses all the vertices.
The function checks if there are no output arguments (nargout==0). If true, it visualizes the result using SGfigure and VLFLplot functions, setting the view to an angle of (-30, 30) degrees.

This function is useful for generating 3D printable models by defining the geometry of a solid object through its bounding box.

Algorithm explaination created using ChatGPT on 2025-08-19 00:47. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21