collofBBs
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Geometric Queries
Introduced first in SolidGeometry 4.0, Creation date: 2017-08-01, Last change: 2025-09-14
Fundamental fnct to retur from two bounding box list the colliding index lists
Description
This function can be used directly to preprocess, i.e. accelerate facet crossing functions
See Also: VLDLBBofVLFL
Example Illustration
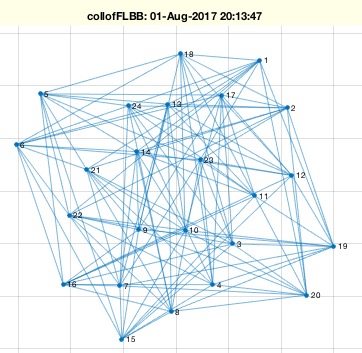
Syntax
[CL,ca,cb]=collofBBs(bba,bbb,[first])
Input Parameter
bba: | | bounding box list A |
bbb: | | bounding box list B |
first: | | if true; function stops after first hit; default is false |
Output Parameter
CL: | | Crossing list [n x 2] = [ia ib] |
ca: | | optional list of crossing boxes in A; ca=unique(CL(:,1),'stable'); |
cb: | | optional list of crossing boxes in B; cb=unique(CL(:,2),'stable'); |
Examples
A=SGbox([30,20,10]);
[~,~,~,~,~,~,bb]=VLDLBBofVLFL(A.VL,A.FL,1)
collofBBs(bb,bb)
Copyright 2017-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, collofBBs, is designed to identify intersecting bounding boxes from two lists, bba and bbb. It is part of the SG-Library and was created by Tim Lueth. The function is useful for preprocessing tasks, such as accelerating facet crossing functions.
Input Parameters
- bba: A list of bounding boxes, referred to as list A.
- bbb: A list of bounding boxes, referred to as list B.
- first: An optional boolean parameter. If set to true, the function stops after finding the first intersecting pair. The default value is false.
Output Results
- CL: A list of intersecting pairs, represented as an
[n x 2] matrix, where each row contains indices [ia ib] indicating intersecting boxes from bba and bbb.
- ca: An optional list of unique indices of intersecting boxes in
bba.
- cb: An optional list of unique indices of intersecting boxes in
bbb.
Algorithm Steps
- Initialize the
first parameter using getfuncparams to determine if the function should stop after the first intersection.
- Determine the number of bounding boxes in
bba and bbb using size.
- Initialize an empty list
CL to store intersecting pairs.
- Iterate over each bounding box in
bba (outer loop) and bbb (inner loop).
- For each pair of bounding boxes, check if they intersect using the condition:
- Check if the maximum x, y, or z coordinate of one box is less than the minimum x, y, or z coordinate of the other box.
- If none of these conditions are true, the boxes intersect.
- If an intersection is found, increment the counter
n and store the indices in CL.
- If
first is true and an intersection is found, break out of the loops.
- After completing the loops, trim
CL to only include valid entries up to n.
- If additional output arguments are requested, compute
ca and cb as unique lists of intersecting indices from bba and bbb, respectively.
- If no output arguments are specified, create an edge list
EL and visualize it using graphofEL.
Algorithm explaination created using ChatGPT on 2025-08-19 08:29. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21