crossC2P
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analyzing function
Introduced first in SolidGeometry 1.0, Creation date: 2012-05-12, Last change: 2025-09-14
returns how often a line crosses a contour
Description
This procedures uses cross4P to test all segments of the vertex list for crossings. The vertex list will be always considered as closed
See Also: PLcross2Lines
, PLcrossCPLline
, iscrossingCPL
, cross4P
Example Illustration
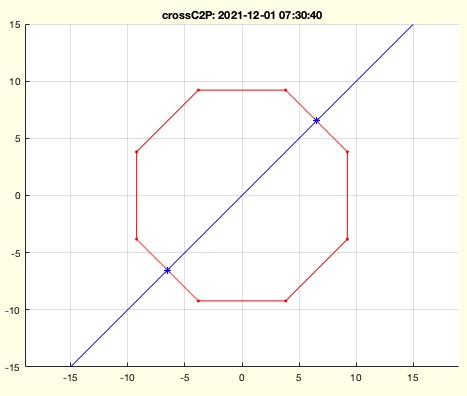
Syntax
[k,CL,CCL]=crossC2P(VL,p1,p2)
Input Parameter
VL: | | vertex list of the contour |
p1: | | start point |
p2: | | end point |
Output Parameter
k: | | number of crossings |
CL: | | [i index of VL, k value distance p2 to p1, k value distance VL(i+1)-VL(i) |
CCL: | | Cross point list |
Examples
crossC2P(PLcircle(10,8),[-15 -15 ],[15 15])
Copyright 2012-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, crossC2P, calculates how often a line crosses a closed contour defined by a vertex list. It uses another function, cross4P, to determine crossings for each segment of the contour.
Input Parameters
- VL: A matrix representing the vertex list of the contour. Each row corresponds to a vertex point in 2D space.
- p1: A 1x2 vector representing the start point of the line.
- p2: A 1x2 vector representing the end point of the line.
Output Results
- k: The number of times the line crosses the contour.
- CL: A matrix where each row contains:
- Index of the vertex in
VL where the crossing occurs.
- Parameter
ka representing the relative distance from p1 to the crossing point along the line.
- Parameter
kb representing the relative distance from the vertex to the crossing point along the contour segment.
- CCL: A list of crossing points in 2D space.
Algorithm Steps
- Determine the number of vertices
n in the vertex list VL.
- Close the contour by appending the first vertex to the end of
VL.
- Initialize
CL as a zero matrix with n rows and 3 columns.
- Initialize counters
k and m to zero.
- Loop through each segment of the contour:
- Call
cross4P to check if the line (p1, p2) crosses the segment (VL(i), VL(i+1)).
- If a crossing is detected (
kc > 0), increment k by kc and m by 1.
- Store the crossing information in
CL.
- Trim
CL to only include detected crossings.
- Calculate the vector
p21 as the difference between p2 and p1.
- Compute the crossing points
CCL using the parameter ka and the vector p21.
- Remove duplicate crossing points from
CCL and update CL accordingly.
- Set
k to the number of unique crossing points.
- If no output arguments are specified, plot the contour, line, and crossing points using graphical functions.
Algorithm explaination created using ChatGPT on 2025-08-19 08:29. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21