diffangle
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Geometric Queries
Introduced first in SolidGeometry 4.0, Creation date: 2017-07-06, Last change: 2025-09-14
3D fnct: calculates the angle between to normal vector lists
Description
in contrast to 2D (acos2) there is no sign in 3D
optimal for list processing. if normalization is required, the time is about doubled
See Also: acos2
, TR3neighborsAngle
, PLangle
, VLangle
, PLangle2
Example Illustration
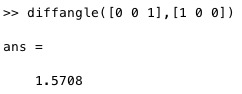
Syntax
[AL,DA]=diffangle(NL1,NL2,[normfirst])
Input Parameter
NL1: | | normal vector lists 1 |
NL2: | | normal vector lists 2 |
normfirst: | | if true; VLnorm is sued to norm the vectors first; |
Output Parameter
AL: | | real(acos(dot(NL1(i,:),NL2(i,1)))) |
DA: | | DA=abs(abs(pi/2-AL)-pi/2) |
Examples
NL1=rand(10,3); NL2=rand(10,3);
Copyright 2017-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, diffangle, calculates the angle between two lists of 3D normal vectors. It is designed for efficient list processing and can optionally normalize the vectors before calculation.
Input Parameters
- NL1: A list of normal vectors (first set).
- NL2: A list of normal vectors (second set). If it contains only one vector, it is replicated to match the size of
NL1.
- normfirst: An optional boolean parameter. If true, the vectors are normalized using
VLnorm before calculating the angle. This step approximately doubles the computation time.
Output Results
- AL: A list of angles in radians, calculated using the arccosine of the dot product of corresponding vectors from
NL1 and NL2.
- DA: An optional output representing the absolute deviation of the angle from 90 degrees.
Algorithm Steps
- Check if
NL1 contains only one element. If so, an error is raised suggesting the use of diffanglew instead.
- Initialize
normfirst to false. If a third argument is provided and is not empty, set normfirst to its value.
- If
NL2 has only one row, replicate it to match the number of rows in NL1.
- If
normfirst is true, normalize both NL1 and NL2 using VLnorm.
- Initialize
AL as a NaN array with the same number of rows as NL1.
- For each pair of vectors from
NL1 and NL2, calculate the angle using the arccosine of their dot product. Store the result in AL.
- Round the values in
AL to six decimal places using rounddiv.
- If a second output is requested, calculate
DA as the absolute deviation of the angle from 90 degrees.
Algorithm explaination created using ChatGPT on 2025-08-19 07:58. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21