diffanglew
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Geometric Queries
Introduced first in SolidGeometry 5.1, Creation date: 2021-03-15, Last change: 2025-09-15
returns the shortest distance from angle 1 to angle 2
Description
also imp
See Also: diffT
, TLadjustR
, diffTrotz
, diffTincz
Example Illustration
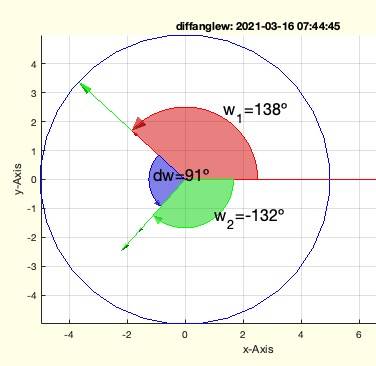
Syntax
dw=diffanglew(w1,w2)
Input Parameter
w1: | | angle w1 |
w2: | | angle w2 |
Output Parameter
dw: | | shortes turning angle from w1 to w2 |
Examples
diffanglew(-2.4,+2.3);
diffanglew(+2.4,-2.3);
diffanglew(+12.4,-2.3);
Copyright 2021-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function calculates the shortest angular distance between two angles, w1 and w2, in radians. The angles are adjusted to be within the range of -À to À, which corresponds to -180 to 179 degrees.
Input Parameters
- w1: The first angle in radians.
- w2: The second angle in radians.
Output
- dw: The shortest turning angle from w1 to w2 in radians.
Algorithm Steps
- Adjust w1 and w2 to be within the range of -À to À using the modulus operation:
- w1 = mod(w1 + À, 2À) - À
- w2 = mod(w2 + À, 2À) - À
- Store the original value of w2 in w2o for later use.
- If w2 is less than w1, add 2À to w2 to ensure the angle is measured in the positive direction.
- Calculate the difference dw as w2 - w1.
- If dw is greater than À, adjust dw by subtracting 2À to ensure the shortest path is taken.
- If no output is requested (nargout == 0), plot the angles and the difference using a graphical representation:
- Draw a circle with radius r/2.
- Plot w1 as a red line and w2 as a green line from the origin.
- Plot the difference dw as a blue arc.
- Label the angles and the difference in degrees.
Algorithm explaination created using ChatGPT on 2025-08-19 07:16. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21