minspanedges
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - EL/Edge Lists
Introduced first in SolidGeometry 4.4, Creation date: 2019-01-07, Last change: 2025-09-14
RETURNS the minimal spanning tree required for Kirchhoff loops (Mesh equations)
Use carefully: The 'minspanedges' function has not yet been extensively tested
Example Illustration
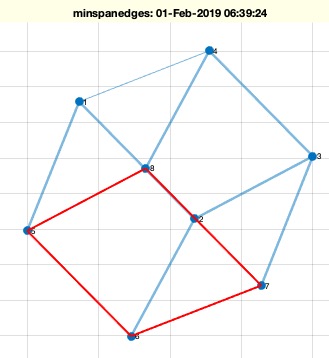
Syntax
[EL,T,KL]=minspanedges(G)
Input Parameter
Output Parameter
EL: | | Edge list |
T: | | Tree |
KL: | | |
Examples
FEofSG(SGbox); EL=ans; G=graph(EL(:,1),EL(:,2))
minspanedges(G), [e,t,l]=minspanedges(G)
Copyright 2019-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This algorithm is designed to compute the minimal spanning tree required for Kirchhoff loops (Mesh equations) from a given graph or digraph. Below is a detailed explanation of the algorithm and its parameters.
Input Parameters
- G: This is the input graph or digraph. It can be an instance of either the 'graph' or 'digraph' class in MATLAB.
Output Results
- EL: Edge list of the graph after processing.
- T: The minimal spanning tree of the graph.
- KL: A cell array containing the Kirchhoff loops.
Algorithm Steps
- Check if the input
G is a digraph. If so, convert its edges to an array and then convert G to an undirected graph using these edges.
- Extract the edge list
EL from the graph G.
- Compute the minimal spanning tree
T of the graph G using the minspantree function.
- Replace
T with the shortest path tree starting from node 3 using the shortestpathtree function.
- Update
EL to the edge list of the tree T.
- Remove the edges of
T from G to create a new graph G1.
- Extract the edge list
EL from G1.
- Initialize a cell array
KL to store Kirchhoff loops.
- For each edge in
EL, compute the shortest path in T between the two nodes of the edge and store it in KL.
- If no output arguments are specified, plot the graph
G and highlight the tree T. Also, plot the edges in EL and the Kirchhoff loops in KL.
Algorithm explaination created using ChatGPT on 2025-08-19 01:40. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21