BBgrow

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 4.5, Creation date: 2019-03-16, Last change: 2025-09-14

increases the size of a Boundary Box

Description

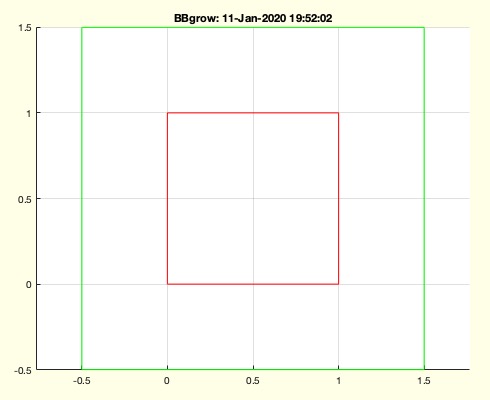
in contrast to BBaddtolerance , this function BBgrowdoes not add a tolerance but magnify the BB.
this function is NOT able to handle lists of BBs yet!

See Also: , BBofSG , BBaddtolerance

Example Illustration

Syntax

nbb=BBgrow(bb,m)

Input Parameter

`bb`:		bounding box or axis
`m`:		growing factor

Output Parameter

nbb: new bounding box

Examples


BBgrow([0 1 0 1 ],1) % unchanged
BBgrow([0 1 0 1 ],2) % magnified around the center
BBgrow([0 1 0 1 0 1],2) % magnified around the center

Copyright 2019-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, BBgrow, is designed to increase the size of a bounding box (BB) by a specified growing factor. It is part of the SolidGeometry library and was introduced in version 4.5. The function does not add a tolerance but magnifies the bounding box around its center.

Input Parameters

bb: A vector representing the bounding box or axis. It can be in 2D (four elements) or 3D (six elements).
m: A scalar representing the growing factor by which the bounding box is magnified.

Output

nbb: A vector representing the new, magnified bounding box.

Algorithm Steps

Calculate the half-width (sx) and center (mx) of the bounding box in the x-direction:
- sx = (bb(2) - bb(1)) / 2
- mx = 0.5 * (bb(2) + bb(1))
Calculate the half-height (sy) and center (my) of the bounding box in the y-direction:
- sy = (bb(4) - bb(3)) / 2
- my = 0.5 * (bb(3) + bb(4))
Compute the new bounding box for 2D:
- nbb = [mx - m * sx, mx + m * sx, my - m * sy, my + m * sy]
If the bounding box is 3D (more than four elements):
- Calculate the half-depth (sz) and center (mz) in the z-direction:
  - sz = (bb(6) - bb(5)) / 2
  - mz = 0.5 * (bb(6) + bb(5))
- Extend the new bounding box to include the z-dimension:
  - nbb = [nbb, mz - m * sz, mz + m * sz]
If no output is requested (nargout == 0), visualize the original and new bounding boxes:
- For 2D bounding boxes, use CPLplot to plot the original in red and the new in green.
- For 3D bounding boxes, use SGplotalpha to plot the original in red and the new in green with transparency.

Algorithm explaination created using ChatGPT on 2025-08-19 06:48. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21