RLofEulerInterpolation
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 3.1, Creation date: 2016-12-02, Last change: 2025-09-14
Returns euler rotations as linear interpolation
Description
Creates Euler rotation list (ZYX) for a linear turning interpolation along a path in 3D. The ez vector is always in the direction of the path. There will be a warning of the path does not fulfill the condition that the euler angle fits to the direction.
VLinsertEulerSteps hast to be called afterwards if there is twist on long distances
See Also: VLinsertEulerSteps
, RL2exl
, VLinsertEulerSteps
, VLradialEdges
, TofPez
Example Illustration
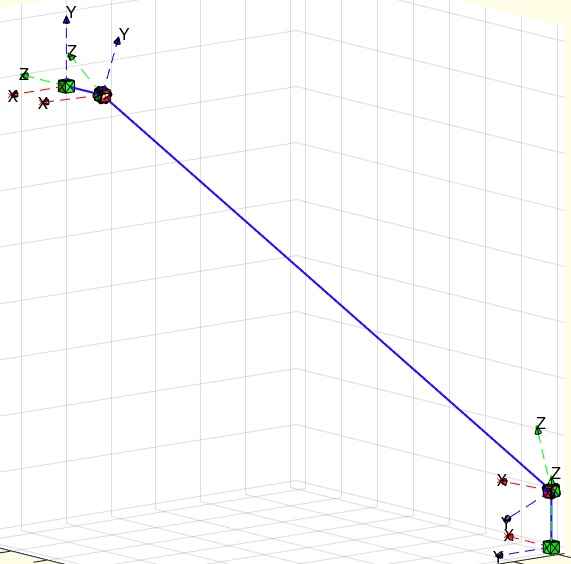
Syntax
[RL,L,DL,NL,EXL]=RLofEulerInterpolation(VL,e1,e2)
Input Parameter
VL: | | Vertex list (nx3) or scalar n |
e1: | | ZYX-Euler angle for first Vertex VL(1,:) or matrix T1,R1 |
e2: | | ZYX-Euler angle for last Vertex VL(end,:) or matrix T2,R2 |
Output Parameter
RL: | | Rotation list of euler angles (n x 3) |
L: | | Length of path, scalar |
DL: | | Distance vector; last one closes (n x 3) |
NL: | | Norm of distance vectors (n x 1) |
EXL: | | Optional List of |
Examples
Just try
VL=[0 0 0; 0 0 10; 40 40 40; 50 40 40];
RLofEulerInterpolation(VL,[0 0 0],[0 pi/2 0])
VL=[0 0 0; 0 0 10; 40 0 10; 40 0 0];
RLofEulerInterpolation(VLradialEdges(VL),[0 0 0],[0 0 pi])
Copyright 2016-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Last html export of this page out of FM database by TL: 2025-09-21