RLplot
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 3.1, Creation date: 2016-12-04, Last change: 2025-09-14
plots along the z axis the systems of a Euler Rotation List
Example Illustration
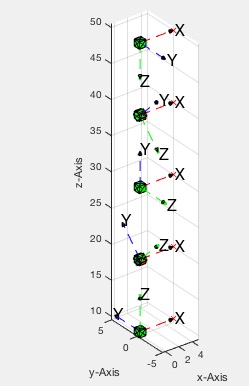
Syntax
RLplot(RL,[VL])
Input Parameter
RL: | | Euler Angle Rotation List |
VL: | | Vertex list or distance between points |
Examples
Simple Rotation
RL=RLofEulerInterpolation(5,[0 0 0],[pi 0 0] )
RLplot(RL)
Copyright 2016-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, RLplot, is designed to plot a series of rotations along the z-axis using Euler angles. It is part of the SG-Library and was created by Tim Lueth. The function takes in two parameters: RL and an optional VL.
Input Parameters
- RL: This is the Euler Angle Rotation List. It contains the rotation angles that will be applied to the plot.
- VL: This is an optional parameter. It can be a vertex list or a distance between points. If not provided, it defaults to 10.
Algorithm Steps
- The function checks if the
VL parameter is provided. If it is not provided or is empty, it defaults to 10.
- The number of rotations,
ni, is determined by the number of rows in the RL matrix.
- The function iterates over each rotation in the
RL list.
- For each rotation, it calculates the transformation using the
TofPEul function, which takes a position vector and the current rotation angles.
- The
tplot function is then called to plot the transformation, with the length parameter set to half of VL.
Example
An example of using this function is provided in the comments:
RL = RLofEulerInterpolation(5, [0 0 0], [pi 0 0]);
RLplot(RL);
This example creates a rotation list using RLofEulerInterpolation and then plots it using RLplot.
Algorithm explaination created using ChatGPT on 2025-08-18 22:03. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21