SGofCPLbendonadrum

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - SG/Solids
Introduced first in SolidGeometry 4.8, Creation date: 2019-12-31, Last change: 2025-09-14

bends a CPL pattern into a cylindrical body (slowly) or rolls it onto a drum

Description

required for example to implement patient specific stents.
The OUTER radius is always the (y-dimension - overlap) / 2 / pi


See Also: SGbending , CPLstentline , CPLstent

Example Illustration

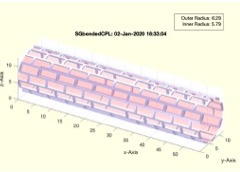
missing image of SGofCPLbendonadrum(CPLN,h,ol,res)

Syntax

SGB=SGofCPLbendonadrum(CPLN,[h,ol,res])

Input Parameter

CPLN: Contour to bend
h: height of the material in z
ol: overlap; default is 0
res: resolution for CPL mesh grid; default is r/10

Output Parameter

SGB: Solid Geometry

Examples


SGofCPLbendonadrum(PLsquare([10,20]),.5);
CPLstent([5 5 5 5 10 5 5 5 5],2,.5,17); X=ans;
SGofCPLbendonadrum(X,.5)



Copyright 2019-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, SGofCPLbendonadrum, is designed to bend a contour pattern (CPL) into a cylindrical shape or roll it onto a drum. It is part of the Solid Geometry Library (SG-Lib) and is used for applications such as creating patient-specific stents.

Input Parameters

Output

Algorithm Steps

  1. Calculate the bounding box of the CPL using BBofCPL and determine the length in the y-dimension (ly).
  2. Retrieve the height h from the input parameters or use the default value of 0.5.
  3. Retrieve the overlap ol from the input parameters or use the default value equal to h.
  4. Calculate the outer radius r using the formula: r = (ly - ol) / (2 * pi).
  5. Determine the diameter increment di using the formula: di = 2 * pi * r / nofrd(r) / 2.
  6. Set the resolution res to [di, di] or retrieve it from the input parameters.
  7. Flip the CPL pattern horizontally using fliplr.
  8. Create a Delaunay grid of the CPL using SGofCPLzdelaunayGrid with the specified height and resolution.
  9. Bend the grid into a cylindrical shape using SGbending with the calculated radius and height.
  10. Rotate the bent geometry around the z-axis by -90 degrees using SGrotate.
  11. Translate the geometry using SGtrans1.
  12. Create a cylinder with the inner radius r-h and the height equal to the x-dimension of the bounding box.
  13. Rotate the cylinder around the y-axis by -90 degrees and align it with the bent geometry using SGtransrelSG.
  14. If no output is requested, plot the resulting geometry using SGfigure and SGplotalpha, and annotate the plot with the outer and inner radii.
Algorithm explaination created using ChatGPT on 2025-08-19 08:29. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21