TmirrorTxy
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Kinematics and Frames
Introduced first in SolidGeometry 5.2, Creation date: 2022-05-01, Last change: 2025-09-15
mirrors frames or cell list of frames
Description
used in SGmirrorTxy
See Also: SGmirrorTxy
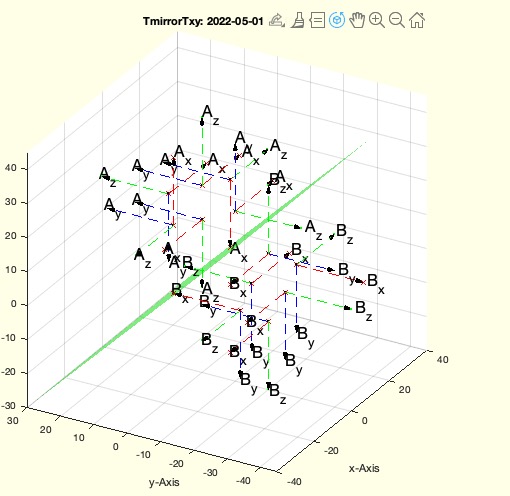
Example Illustration
Syntax
TB=TmirrorTxy(TA,[T])
Input Parameter
TA: | | frame or cell list of frames to be mirrored |
T: | | mirror axis is given by ez, T, ez, 'x' |
Output Parameter
TB: | | mirrored fram of mirrored frame list |
Copyright 2022-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, TmirrorTxy, mirrors frames or a list of frames across a specified mirror axis. It is part of the SG-Library and was developed by Tim Lueth.
Input Parameters
- TA: A frame or a cell list of frames that need to be mirrored.
- T: The mirror axis, which can be specified as 'ez', T, ez, or 'x'. This parameter is passed as a second argument in the function call.
Output
- TB: The mirrored frame or list of mirrored frames.
Algorithm Steps
- Check if
TA is empty. If it is, return TA as TB and exit the function.
- Retrieve the mirror axis
T using getfuncparams. If T is empty, throw an error indicating that a mirror plane is required.
- If
T is a character, convert it to a transformation matrix using TofPez and ezofchar.
- If
TA is a cell array, iterate over each element and recursively call TmirrorTxy for each frame, storing the result in TB.
- If
TA is not a cell array, perform the following operations:
- Transform
TA using the inverse of T.
- Negate the third row of the transformed matrix to achieve mirroring.
- Transform the matrix back using
T.
- Ensure orthogonality by recalculating the first column as the cross product of the second and third columns.
- If no output arguments are specified, visualize the results using
SGfigure, tfplot, and tplot functions.
Algorithm explaination created using ChatGPT on 2025-08-19 00:54. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21