TofPL

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - CPL/Closed Polygon Lists
Introduced first in SolidGeometry 4.4, Creation date: 2018-12-28, Last change: 2025-09-14

returns a 2D HT matrix for a point list

See Also: TofR , TofVL , TPL , TofDPhiH , T3ofT2 , Tof3P , T2P , TofP , TofPLpath

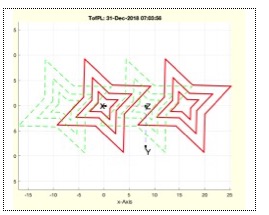
Example Illustration

Syntax

T=TofPL(PL)

Input Parameter

PL: Point list

Output Parameter

T: 3x3 HT matrix

Examples


TofPL(CPLsample(14))

Copyright 2018-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, TofPL, computes a 2D homogeneous transformation (HT) matrix for a given point list (PL). The function is part of the SolidGeometry library and is used to transform closed polygon lists.

Input Parameters

PL: A point list, which is a matrix where each row represents a point in 2D space.

Output Results

T: A 3x3 homogeneous transformation matrix.
ew: Eigenvalues of the covariance matrix, adjusted by a factor of sqrt(2).

Algorithm Steps

Remove any rows in PL that contain NaN values to ensure clean data.
Calculate the number of points, n, in the cleaned point list.
Compute the mean of the points. If there is more than one point, use the mean; otherwise, use the single point as the mean.
Initialize a variable K to zero. This will store the covariance matrix.
Iterate over each point in the list to compute the covariance matrix K:
- For each point, calculate the outer product of the difference between the point and the mean.
- Accumulate this value into K.
Normalize K by dividing by n and the square root of n.
Compute the eigenvectors V and eigenvalues ew of the covariance matrix K using the condeig function.
Reorder the eigenvalues and adjust them by dividing by sqrt(2).
Construct the transformation matrix T using the eigenvectors and the mean of the points.
If no output is requested, plot the original and transformed point lists for visualization.

Example Usage

To use the function, call it with a point list, such as TofPL(CPLsample(14)).

Algorithm explaination created using ChatGPT on 2025-08-19 00:12. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21