TofRd
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Kinematics and Frames
Introduced first in SolidGeometry 5.3, Creation date: 2023-03-11, Last change: 2025-09-15
creates a frame after rotation in distance d along new ex
Description
In contrast to TofR, this function has the point in distance d along ex
See Also: TofR
Example Illustration
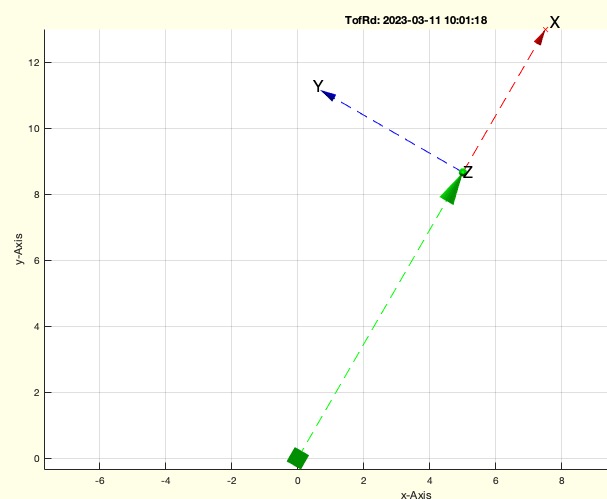
Syntax
TR=TofRd([w,d,e])
Input Parameter
w: | | rotation angle or rotation vector |
d: | | distant along dx |
e: | | direction; default is 'x'; not used yet |
Output Parameter
Examples
TofRd([pi/3],10)
TofRd([0 0 pi/3],10)
TofRd([0 pi/4 pi/3],10)
Copyright 2023-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, TofRd, is designed to create a transformation matrix (HT matrix) after applying a rotation and translation along a specified axis. It is part of the SG-Library and is used in kinematics and frames.
Input Parameters
- w: This parameter represents the rotation angle or rotation vector. It can be a single angle or a vector specifying rotation about the x, y, and z axes.
- d: This is the distance along the x-axis (dx) after rotation.
- e: This parameter specifies the direction, with a default value of 'x'. However, it is not used in the current implementation.
Output
- TR: The output is a homogeneous transformation (HT) matrix.
Algorithm Steps
- The function begins by retrieving the input parameters using the
getfuncparams function. Default values are set for each parameter: w defaults to pi/10, d defaults to 0, and e defaults to 'x'.
- The rotation matrix
R is calculated using the rot function, which processes the rotation vector or angle w.
- The function checks the size of the rotation matrix
R to determine the appropriate transformation matrix format:
- If
R is a 2x2 matrix (4 elements), the transformation matrix T is constructed as a 3x3 matrix with the translation along the x-axis.
- If
R is a 3x3 matrix (9 elements), the transformation matrix T is constructed as a 4x4 matrix with the translation along the x-axis.
- If
R does not match these sizes, an error is raised indicating a wrong format.
- The resulting transformation matrix
T is assigned to the output variable TR.
- If no output is requested (
nargout==0), the function visualizes the transformation using SGfigure, lplot, and tplot functions. It converts a 3x3 matrix to a 4x4 matrix if necessary using T3ofT2.
Algorithm explaination created using ChatGPT on 2025-08-19 00:14. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21