TofT
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 4.1, Creation date: 2017-08-20, Last change: 2025-09-14
returns a T matrix defined relative to another T matrix
Description
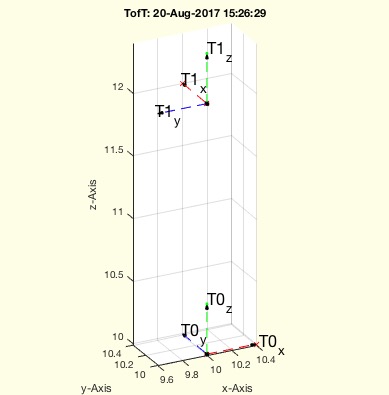
This function help to specify a new matrix relative to an existing one. This is helpful to define cutting planes for SGcutT for example.
In fact it is the same as T1=T0*TofR(R,P) but may be easier to understand.
See Also: TofR
, TofVL
, TPL
, TofDPhiH
, T3ofT2
, Tof3P
, T2P
, TofP
, TofPez
, TofPEul
, TofTrel
Example Illustration
Syntax
T1=TofT(T0,[R,P])
Input Parameter
T0: | | Original Matrix |
R: | | Rotation matrix relative to the T axis; scalar=phiz |
P: | | Translation vector relative to the T axis; scalar=z |
Output Parameter
T1: | | resulting new T Matrix |
Examples
TofT(TofP([10 10 10]),10)
TofT(TofP([10 10 10]),rot(0,0,pi))
TofT(TofP([10 10 10]),pi/2,2)
Copyright 2017-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, TofT, is designed to compute a new transformation matrix T1 relative to an existing transformation matrix T0. It is part of the SolidGeometry library and is useful for defining new coordinate systems or transformation matrices, particularly in applications like defining cutting planes.
Input Parameters
- T0: The original transformation matrix, a 4x4 matrix representing the initial coordinate system.
- R: A rotation matrix or scalar. If a scalar is provided, it represents a rotation around the z-axis (phiz). If a matrix is provided, it should be a 3x3 rotation matrix.
- P: A translation vector or scalar. If a scalar is provided, it represents a translation along the z-axis. If a vector is provided, it should be a 3-element vector representing translation along the x, y, and z axes.
Output
- T1: The resulting transformation matrix, a 4x4 matrix that represents the new coordinate system after applying the specified rotation and translation to T0.
Algorithm Steps
- Initialize the rotation matrix R to the identity matrix if not provided.
- Initialize the translation vector P to zero if not provided.
- Check if R is a scalar. If so, convert it to a rotation matrix using the rot function, assuming a rotation around the z-axis.
- If R is not a square matrix, assume it is a vector and convert it to a rotation matrix using the rot function.
- Check if P is a scalar. If so, convert it to a 3-element vector with the scalar as the z-component.
- Initialize T1 as a copy of T0.
- Update the translation part of T1 by adding the product of T0's rotation part and the translation vector P to T0's translation part.
- Update the rotation part of T1 by multiplying it with the rotation matrix R.
- If no output is requested, visualize the original and resulting transformation matrices using the SGfigure and tplot functions.
Example Usage
TofT(TofP([10 10 10]),10): Applies a rotation of 10 radians around the z-axis to the transformation matrix obtained from the point [10, 10, 10].TofT(TofP([10 10 10]),rot(0,0,pi)): Applies a rotation of pi radians around the z-axis to the transformation matrix obtained from the point [10, 10, 10].TofT(TofP([10 10 10]),pi/2,2): Applies a rotation of pi/2 radians around the z-axis and a translation of 2 units along the z-axis to the transformation matrix obtained from the point [10, 10, 10].
Algorithm explaination created using ChatGPT on 2025-08-19 08:29. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21