VLBeziernoose
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - SG/Solids
Introduced first in SolidGeometry 1.0, Creation date: 2012-05-20, Last change: 2025-09-14
returns a Point list of a noose as link between 2 points with a desired spring length
Description
The procedure uses the concept of: Gunter Erhard (2008): "Konstruieren mit Kunststoffen [Design for Polymers]", Hanser Verlag, Muenchen, 4. Auflage, p.
Example Illustration
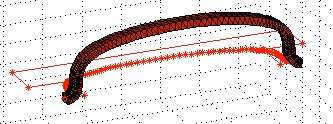
Syntax
VL=VLBeziernoose(d,h,b,a,n)
Input Parameter
d: | | length in x |
h: | | half of the height in y |
b: | | upper neck of the noose |
a: | | lower neck of the noose |
n: | | number of points |
Output Parameter
VL: | | Point list as vertex list |
Examples
Create a Noose:
[VL,PL]=VLBeziernoose (60,10,5,5,100);VLFLfigure; VLplot(VL), VLplot (PL)
[NVL,NFL]=VLFLexpandPL (VL',2,3); NVL=VLswapYZ(NVL); VLFLplot (NVL,NFL)
Copyright 2012-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
The function VLBeziernoose generates a list of points representing a noose shape using Bezier curves. It is designed to create a smooth transition between two points with a specified spring length.
Input Parameters
- d: Length in the x-direction. It determines the horizontal span of the noose.
- h: Half of the height in the y-direction. It defines the vertical extent of the noose.
- b: Upper neck of the noose. It specifies the width at the top of the noose.
- a: Lower neck of the noose. It specifies the width at the bottom of the noose.
- n: Number of points. It determines the resolution of the point list, with more points resulting in a smoother curve.
Output Results
- VL: A point list (vertex list) representing the noose shape.
- PL: Control points used to generate the Bezier curve.
Algorithm Steps
- Define the control points
PL for the Bezier curve. These points outline the shape of the noose:
- Start at the origin (0,0,0).
- Move to the upper neck (b,0,0).
- Ascend vertically to (b,h,0).
- Move horizontally to the left to (0-a,h,0).
- Ascend further to (0-a,2*h,0).
- Move horizontally to the right to (d+a,2*h,0).
- Descend to (d+a,h,0).
- Move horizontally to the left to (d-b,h,0).
- Descend to (d-b,0,0).
- End at (d,0,0).
- Call the function
VLBezierC with the control points PL and the number of points n to generate the vertex list VL.
Algorithm explaination created using ChatGPT on 2025-08-18 22:44. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21