VLofT
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Kinematics and Frames
Introduced first in SolidGeometry 5.1, Creation date: 2021-03-18, Last change: 2025-09-15
returns the origin T(1:3,4) of a frame list
See Also: VLofSG
Example Illustration
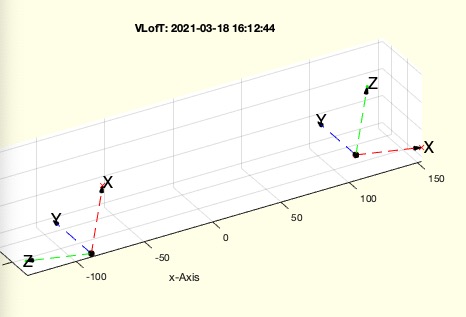
Syntax
VL=VLofT(TL)
Input Parameter
TL: | | [n*4 x 4] list or cell list of 4x4 frames |
Output Parameter
VL: | | vertex list of the frame origins |
Copyright 2021-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, VLofT, is designed to extract the origins of a list of 4x4 transformation matrices, which represent frames in 3D space. The function can handle both regular matrices and cell arrays of matrices.
Input Parameters
- TL: A list or cell list of 4x4 frames. It can be an [n*4 x 4] matrix or a cell array containing these matrices.
Output Results
- VL: A vertex list of the frame origins. This is a list of the translation components (the last column) of each 4x4 matrix in the input.
Algorithm Steps
- Store the input
TL in TLO for potential future use.
- Check if
TL is a cell array using iscell(TL):
- If
TL is a cell array:
- Convert the cell array to a regular matrix using
cell2mat(TL).
- Extract the first three rows of the matrix, which correspond to the rotational and translational components.
- Identify the columns that contain the translation vectors (every fourth column) and extract them.
- Transpose the result to get the vertex list
VL.
- If
TL is not a cell array:
- Directly extract the fourth column of each 4x4 matrix, which contains the translation vectors.
- Reshape the extracted data to ensure it is in the correct format.
- Extract the first three rows, which are the x, y, z components of the translation vectors.
- Transpose the result to get the vertex list
VL.
- Use
squeeze(VL) to remove any singleton dimensions.
- If no output argument is specified (
nargout==0), visualize the result:
- Call
SGfigure(-30,30) to set up a figure for plotting.
- Use
hold on to allow multiple plots on the same figure.
- Calculate the size of the bounding box using
sofBB(BBofVL(VL)).
- Plot the frames using
tplot(TL,s/4,'','',''), where s/4 scales the plot.
Algorithm explaination created using ChatGPT on 2025-08-18 22:53. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21