VLswapXZ
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Spatial Relations
Introduced first in SolidGeometry 1.0, Creation date: 2012-05-02, Last change: 2025-09-14
x-axis becomes z-axis of a VL (y-rotation by +90 degree)
Description
y-rotation by +90 degree of a vertex list that [x y z] becomes [-z y x];
This very fast function is used if a 2D drawing is made in x/z and should be used in x/y.
Inverse procedure: VLswapZX(VL)
See Also: VLswapYZ
, VLswapZY
, VLswapXY
, VLswapYX
, VLswapZX
, VLswapX
, VLswapY
, VLswapZ
Example Illustration
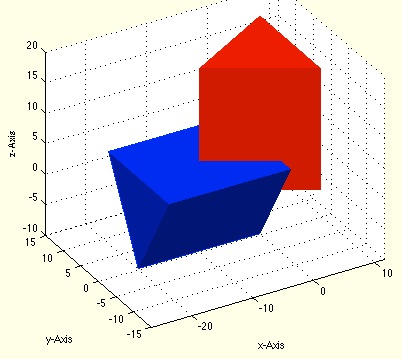
Syntax
RVL=VLswapXZ(VL)
Input Parameter
Output Parameter
RVL: | | Rotated vertex list. |
Copyright 2012-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This algorithm is a function named VLswapXZ from the SG-Library, designed to perform a specific transformation on a list of vertices. The function is used to rotate a 3D vertex list by +90 degrees around the y-axis, effectively swapping the x and z coordinates.
Input Parameters
- VL: The original vertex list, which is a matrix where each row represents a vertex with coordinates [x, y, z].
Output Results
- RVL: The rotated vertex list, where each vertex is transformed such that the x-axis becomes the z-axis. The transformation applied is [x, y, z] becomes [-z, y, x].
Algorithm Explanation
The function VLswapXZ takes a matrix VL as input, where each row represents a vertex in 3D space with coordinates [x, y, z]. The function performs a rotation around the y-axis by +90 degrees. This is achieved by rearranging the columns of the input matrix VL as follows:
- The new x-coordinate is the negative of the original z-coordinate:
-VL(:,3).
- The y-coordinate remains unchanged:
VL(:,2).
- The new z-coordinate is the original x-coordinate:
VL(:,1).
The result is a new matrix RVL, where each vertex has been transformed according to the specified rotation.
This function is particularly useful when a 2D drawing is initially made in the x/z plane and needs to be used in the x/y plane. The inverse procedure to revert this transformation is VLswapZX.
Algorithm explaination created using ChatGPT on 2025-08-18 23:03. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21