code3Byte2single
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 5.0, Creation date: 2020-11-29, Last change: 2025-09-15
converts 3 Bytes plus 8 Bit code into a single
Description
There is a warning if exp/code 0 126 or 127 is used. This is reserver for 0 and 0.5 to
See Also: parts2single
, single2parts
Example Illustration
Syntax
k=code3Byte2single(e,u)
Input Parameter
e: | | code/exponent (no 0, 126, 127) |
u: | | 3 Bytes uint8 |
Output Parameter
k: | | single precision 4 Bytes coded |
Examples
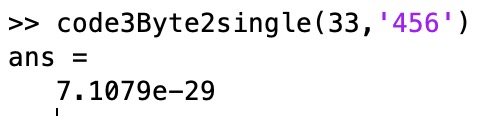
code3Byte2single(33,'456')
[a,b,c,d]=single2parts(code3Byte2single(33,'456')), char(d)
Copyright 2020-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, code3Byte2single, converts a combination of a code/exponent and 3 bytes into a single precision floating-point number. It is part of the SolidGeometry library and was introduced in version 5.0.
Input Parameters
- e: This is the code or exponent. It must not be 0, 126, or 127, as these values are reserved.
- u: This is a 3-byte input, represented as a string of 3 characters, each corresponding to a byte.
Output
- k: The output is a single precision floating-point number, represented in 4 bytes.
Algorithm Steps
- Create a quantizer object for single precision using
quantizer('single').
- Check if the exponent
e is one of the reserved values (0, 126, 127). If so, raise an error.
- Convert the 3-byte input
u into a binary string using dec2bin(uint8(u),8).
- Verify that the binary representation of
u has exactly 3 rows. If not, raise an error.
- Reshape the binary string into a single row vector.
- Extract the sign bit
sb from the first bit of the reshaped binary string.
- Extract the mantissa bits
mb from the next 23 bits of the reshaped binary string.
- Convert the exponent
e into an 8-bit binary string using dec2bin(e,8). If the result has more than 8 bits, raise an error.
- Combine the sign bit, exponent bits, and mantissa bits into a single binary string.
- Convert the combined binary string into a single precision floating-point number using
bin2float(q,[sb eb mb]).
The function ensures that the input parameters are valid and correctly formatted before performing the conversion. It uses binary manipulation to construct the IEEE 754 representation of a single precision floating-point number.
Algorithm explaination created using ChatGPT on 2025-08-19 00:38. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21