single2parts
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 5.0, Creation date: 2020-11-29, Last change: 2025-09-15
returns the parts of a 32 Bit float
See Also: parts2single
, code3Byte2single
Example Illustration
Syntax
[e,m,s,ub]=single2parts(k)
Input Parameter
k: | | single precision number |
Output Parameter
e: | | 8 Bit Exponent mantisse (>1 ==128..255, <1 == 0..128) |
m: | | 23 Bit fraction mantisse |
s: | | sign; 0==1positive 1==negative |
ub: | | 3 uint8 Bytes (sign plus mantisse, 24 Bit) |
Examples
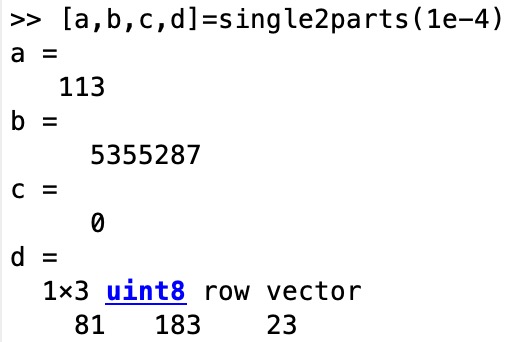
[a,b,c,d]=single2parts(1e-4)
Copyright 2020-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, single2parts, is designed to decompose a 32-bit single precision floating-point number into its constituent parts: the exponent, mantissa, sign, and a 3-byte unsigned integer representation.
Input Parameters
- k: A single precision floating-point number that is to be decomposed.
Output Results
- e: The 8-bit exponent part of the floating-point number. It is extracted from the binary representation of the number.
- m: The 23-bit mantissa (fraction) part of the floating-point number. It is also extracted from the binary representation.
- s: The sign bit of the floating-point number. A value of 0 indicates a positive number, while 1 indicates a negative number.
- ub: A 3-byte unsigned integer array representing the sign and mantissa.
Algorithm Steps
- Create a quantizer object for single precision using
quantizer('single'). This object helps in converting the number to its binary representation.
- Convert the input number
k to its binary representation using num2bin(q,k), where q is the quantizer object.
- Extract the sign bit from the first character of the binary string using
bin2dec(u(1)).
- Extract the exponent from the binary string using
bin2dec(u(2:9)). This gives the 8-bit exponent.
- Extract the mantissa from the binary string using
bin2dec(u(10:end)). This gives the 23-bit fraction.
- If the sign bit
s is greater than 0, negate the mantissa m to reflect the negative sign.
- Convert the mantissa to a 32-bit unsigned integer and then to a 3-byte unsigned integer array using
typecast(uint32(m),'uint8') and fliplr(ub(1:3)) to reverse the byte order.
This function is part of the SolidGeometry library and was introduced in version 5.0. It is useful for understanding the internal representation of single precision floating-point numbers.
Algorithm explaination created using ChatGPT on 2025-08-18 23:22. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21