dofn
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 1.0, Creation date: 2012-12-15, Last change: 2025-09-14
returns the radius relation between a radius and a n-polygon
Description
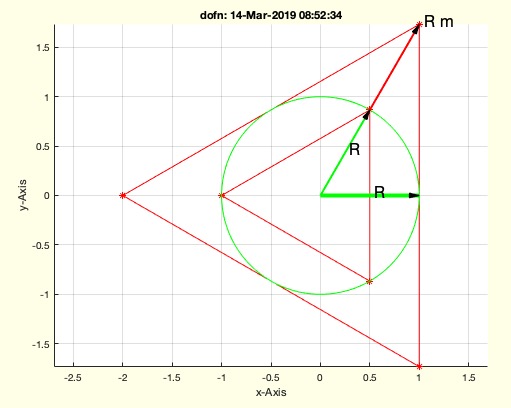
Similar concept as nofrd. If a polygon is created instead of a real circle, either the edges or the points have not the correct distance to the origin.
See Also: nofrd
, sofrd
, phiofsr
, circ2poly
Example Illustration
Syntax
[m,id]=dofn(n)
Input Parameter
Output Parameter
m: | | magnification of the point distance |
id: | | 1/d reduction of the edge distance |
Examples
dofn(6)
Copyright 2012-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, dofn, calculates the relationship between the radius of a circle and the radius of a regular n-sided polygon inscribed in the circle. It is part of the SolidGeometry library and was introduced by Tim Lueth.
Input Parameters
- n: The number of edges of the polygon.
Output Results
- m: The magnification factor of the point distance from the center to the vertices of the polygon.
- id: The inverse of the magnification factor, representing the reduction of the edge distance from the center to the midpoint of the edges.
Algorithm Steps
- Check if
n is empty or zero. If so, set m and id to 1 and return.
- Calculate
m as 1/cos(pi/n), which represents the magnification of the point distance.
- Calculate
id as 1/m, which is the reduction of the edge distance.
- If no output arguments are specified, call the function
circ2poly(n) to visualize the polygon.
Example
Calling dofn(6) will calculate the magnification and reduction factors for a hexagon.
Algorithm explaination created using ChatGPT on 2025-08-18 23:23. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21