erfGauss
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 5.0, Creation date: 2021-01-14, Last change: 2025-09-15
returns the error fnct for the Gaussian distribution
See Also: meanGauss
, erfinvGauss
Example Illustration
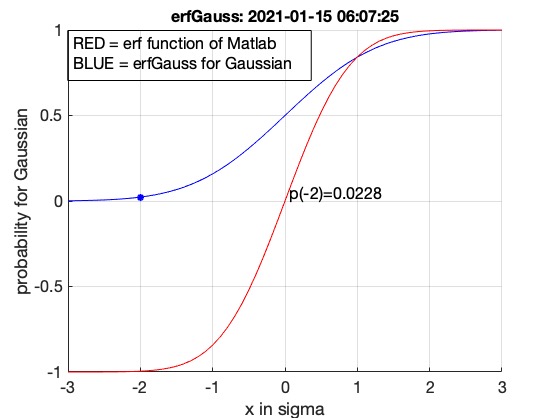
Syntax
y=erfGauss(x)
Input Parameter
x: | | normalized t value (1 = 1 sigma) (X-Xref)/s |
Output Parameter
y: | | error probability (for negative values) |
Examples
erfGauss(-2); SGfigurepapermode
Copyright 2021-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, erfGauss, calculates the error function for the Gaussian distribution. It is part of the SolidGeometry library and was introduced in version 5.0. The function is designed to compute the error probability for a given normalized t-value.
Input Parameters
- x: A normalized t-value, where 1 corresponds to 1 sigma. It is calculated as (X-Xref)/s, where X is the value of interest, Xref is the reference value, and s is the standard deviation.
Output Results
- y: The error probability for negative values of the input x.
Algorithm Steps
- The function calculates the error probability using the formula:
y = 0.5 * (1 + erf(x/sqrt(2))). This formula is derived from the standard error function, adjusted for the Gaussian distribution.
- If the function is called without output arguments, it enters a visualization mode:
- It creates a range of values from -3 to 3 with a step of 0.1.
- It plots the
erfGauss function in blue and the standard erf function in red for comparison.
- Annotations are added to the plot to distinguish between the two functions.
- The specific point (x, y) is marked with a blue star on the plot.
- A text annotation is added to display the probability at the given x value.
- The plot is labeled with appropriate axis labels and the 3D rotation is disabled.
Example Usage
The function can be called with a specific x value, such as erfGauss(-2), to compute the error probability. Additionally, the function can be used in a visualization mode to compare the erfGauss and standard erf functions.
Algorithm explaination created using ChatGPT on 2025-08-18 23:31. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21