getCurrentPoint

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - SimMechanics
Introduced first in SolidGeometry 3.6, Creation date: 2017-03-21, Last change: 2025-08-26

this fnct returns the currentPoint but also the axis limits

Description

% Sometime after ginput or after get(gca,'CurrentPoint' ) the returned
% coordinates are unfortunately not inside of the active axis. This Matlab bug is
% related to changing programmatically the size of the window by a command and
% having at the time the windowchange allowed.
% This fnctn just help to detect the problem. So it is more a debug fnctn.

See Also:

Example Illustration

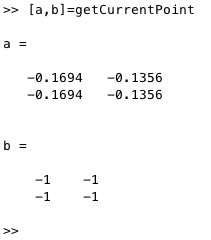
Syntax

[p,ax]=getCurrentPoint

Output Parameter

`p`:		2 point describing the view axis of the last click
`ax`:		axis limits for each point -1 to small + 1 to big 0=inside of view

References

-Ron Pfeifle and Hans-Peter Seidel (1996): GI '96 Proceedings of the conference on Graphics interface '96, Pages 186-193

Copyright 2017-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function, getCurrentPoint, is designed to address a specific issue in MATLAB where the coordinates returned by ginput or get(gca, 'CurrentPoint') may not be within the active axis due to programmatically changing the window size. It serves as a debugging tool to detect this problem.

Input Parameters

The function does not take any input parameters.

Output Results

p: A 2x3 or 2x2 matrix describing the view axis of the last click.
ax: A matrix indicating the axis limits for each point. Values are -1 if the point is too small, +1 if too big, and 0 if inside the view.

Algorithm Steps

Retrieve the current point using get(gca, 'CurrentPoint') and store it in p.
Get the current axis limits using axis(gca) and replicate it to match the size of p, storing the result in ax.
Check if the axis has more than four elements (indicating a 3D plot).
If the axis is 3D:
- Calculate ax for each dimension (x, y, z) using logical conditions to determine if the point is outside the axis limits.
If the axis is 2D:
- Calculate ax for the x and y dimensions only.
- Adjust p to only include the first two columns.

Algorithm explaination created using ChatGPT on 2025-08-19 01:03. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21