hesseplaneofT

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 5.2, Creation date: 2022-06-19, Last change: 2025-09-15

Hessennormalform of T's xy plane

Description

d=planedistanceofT(T,[0 0 0])
The Hesse Normal Form to describe a plane in 3D is a combination of the ez vector of the plane and the distance from the world origin to the plane in the direction of the normal vector.

See Also: planedistanceofT

Example Illustration

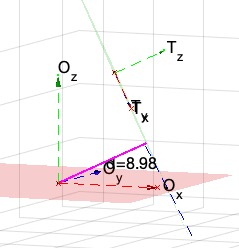
missing image of hesseplaneofT(T,T0)

Syntax

[dh,ez,XL]=hesseplaneofT(T,[T0])

Input Parameter

T: HT Matrix
T0: reference plane default is eye(4)

Output Parameter

dh: hesse distance to plane
ez: ez vector of T
XL: PL that defined the cutting edge

Examples


T=TofPez([4 4 0],[2 +1 1]), hesseplaneofT(T)
T2=T; T2(1:3,4)=T2(1:3,4)+2*T2(1:3,1)+40*T2(1:3,2); hesseplane(T2)
hesseplaneofT(T,T2)



Copyright 2022-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Last html export of this page out of FM database by TL: 2025-09-21