mod1
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Auxiliary function
Introduced first in SolidGeometry 2.5.1, Creation date: 2015-09-16, Last change: 2025-09-14
returns mod fnct for elements 1:k
Description
The standard mod functions works with 0 als starting point, mod1 workswith 1 as starting point
auxiliary function for array manipulation. Instead of return values between [0..k-1], this function returns [1..k] by a=mod(n-1,k)+1
See Also: modN
, mod1circsequ
Example Illustration
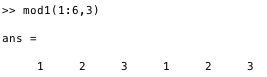
Syntax
a=mod1(n,k,[shft])
Input Parameter
n: | | number |
k: | | divider |
shft: | | default is 1 |
Output Parameter
Examples
mod(1:6,3) % this si the standard mod func
mod1(1:6,3) % an index list of a vector with 3 elements will address the points 1 2 3 1 2 3
Copyright 2015-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function, mod1, is an auxiliary procedure for array manipulation, designed to work similarly to the standard modulus function but with a different starting point. It is part of the SG-Library and was introduced in SolidGeometry 2.5.1.
Input Parameters
- n: The number or array of numbers for which the modulus operation is to be performed.
- k: The divider used in the modulus operation.
- shft: An optional parameter with a default value of 1. It determines the starting point of the modulus operation.
Output
- a: The result of the modulus operation, adjusted to start from 1 instead of 0. The output values range from 1 to k.
Algorithm Explanation
The function mod1 calculates the modulus of a number or array of numbers n with respect to a divider k, but instead of returning values in the range [0..k-1], it returns values in the range [1..k]. This is achieved by adjusting the input number n by a shift value shft (default is 1), performing the modulus operation, and then readjusting the result by adding the shift value back.
Detailed Steps
- Retrieve the shift value using the helper function
getfuncparams, which defaults to 1 if not provided.
- Adjust the input number
n by subtracting the shift value shft.
- Perform the modulus operation with the adjusted number and the divider
k.
- Add the shift value
shft back to the result to ensure the output starts from 1.
Example
Using the standard modulus function, mod(1:6,3) would return [0 1 2 0 1 2]. However, using mod1(1:6,3) returns [1 2 3 1 2 3], effectively creating an index list for a vector with 3 elements.
Algorithm explaination created using ChatGPT on 2025-08-18 23:43. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21