rofRintrusion

by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
Introduced first in SolidGeometry 5.0, Creation date: 2020-12-31, Last change: 2025-09-15

provides the minimum intrusion distance to fully insert a cylinder into a sphere

Description

Better name would be cofarcchord:
a=acos(1-w/R)
r=sin(a)*R

See Also: sofrd , dofRintrusion , PLchordof2PR , Rofrdintrusion

Example Illustration

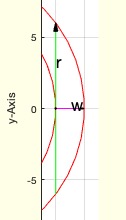
Syntax

r=rofRintrusion(R,w)

Input Parameter

`R`:		Radius of sphere
`w`:		wall thickness of sphere

Output Parameter

r: maximum radius to insert

Examples


rofRintrusion(10,2)

Copyright 2020-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth

Algorithm (Workflow)

This function calculates the maximum radius r that can be inserted into a sphere with a given radius R and wall thickness w. The function is part of the SolidGeometry library and is used for analytical geometry calculations.

Input Parameters

R: Radius of the sphere.
w: Wall thickness of the sphere.

Output

r: Maximum radius that can be inserted into the sphere.

Algorithm Explanation

The function calculates the angle a using the formula:

a = acos(1 - w/R)

This angle a is used to determine the maximum radius r that can be inserted into the sphere:

r = sin(a) * R

Example

For a sphere with a radius of 10 mm and a wall thickness of 2 mm, the function call rofRintrusion(10, 2) will calculate the maximum radius r that can be inserted.

Visualization

If no output arguments are specified, the function will generate a plot to visualize the sphere and the maximum insertion radius. The plot includes:

The outer circle representing the sphere with radius R.
The inner circle representing the sphere with reduced radius R-w.
Lines indicating the maximum insertion distance r.
Annotations showing the values of R, w, and r.

Algorithm explaination created using ChatGPT on 2025-08-19 00:56. (Please note: No guarantee for the correctness of this explanation)

Last html export of this page out of FM database by TL: 2025-09-21