tangentRP
by MATLAB-CENTRAL, SG-Lib Toolbox: SolidGeometry 5.6 - Analytical Geometry
, Creation date: 2015-08-22, Last change: 2025-09-14
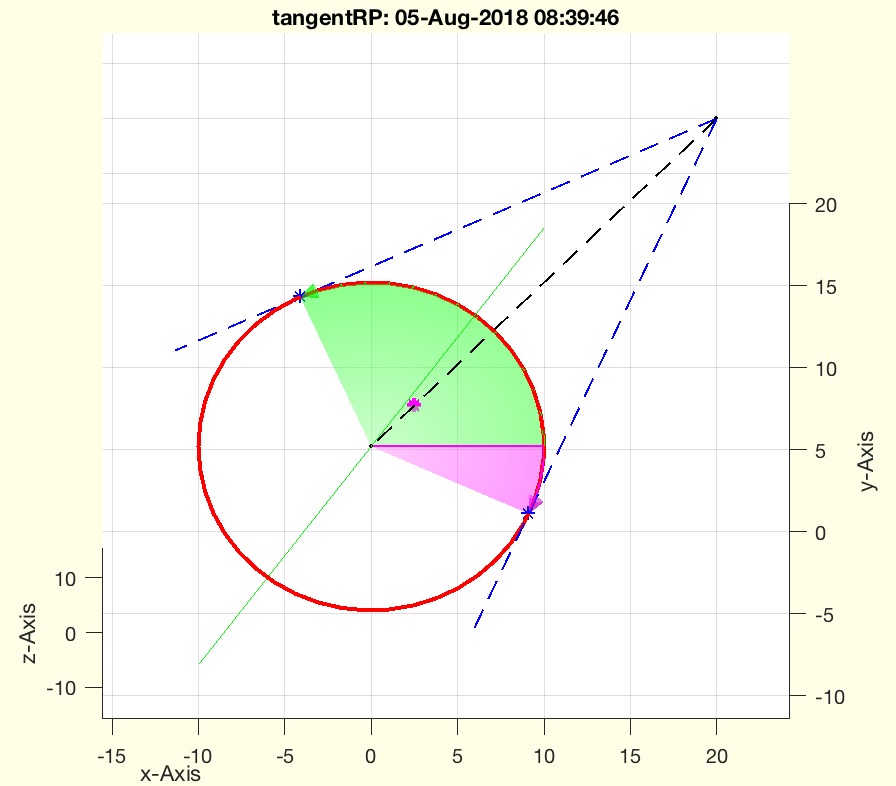
returns the two tangential points of a circle
Description
Thanks to Laurens de Smedt for finding it at MATLAB-Central
See Also: center3P
, center4P
, tangente
Example Illustration
Syntax
[q1,q2,w1,w2]=tangentRP(R,p,[pc])
Input Parameter
R: | | Radius of the circle |
p: | | point to match |
pc: | | optional center of the circle; default is [0 0] |
Output Parameter
q1: | | point 1 (green) |
q2: | | point 1 (magenta) |
w1: | | angle of q1 in world coordinates relative to pc |
w2: | | angle of q2 in world coordinates relative to pc |
Examples
tangentRP(10,[20 20])
This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This function calculates the two tangential points of a circle from a given external point.
Input Parameters
- R: Radius of the circle.
- p: A point from which tangents to the circle are drawn.
- pc (optional): Center of the circle. Default is [0, 0].
Output Results
- q1: First tangential point on the circle.
- q2: Second tangential point on the circle.
- w1: Angle of q1 in world coordinates relative to pc.
- w2: Angle of q2 in world coordinates relative to pc.
Algorithm Steps
- Initialize the center of the circle
pc to [0, 0] unless specified.
- Calculate the vector
p1 from the center pc to the point p.
- Compute the squared distance
d2 and the distance d from pc to p.
- Calculate the point
q0 on the line from pc to p that is closest to the circle.
- Determine the vector
dt that is perpendicular to p1 and scaled by the circle's radius.
- Compute the tangential points
q1 and q2 by adding and subtracting dt from q0.
- Calculate the angles
w1 and w2 of q1 and q2 relative to pc using the atan2 function.
- If no output is requested, plot the circle, points, and tangents for visualization.
Algorithm explaination created using ChatGPT on 2025-08-19 07:33. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21