Poseflip
by Tim C. Lueth, SG-Lib Toolbox: SolidGeometry 5.6 - 4Bar/Linkages
Introduced first in SolidGeometry 5.3, Creation date: 2023-07-24, Last change: 2025-09-15
flips the direction of pose vectors in a Pose struct
Description
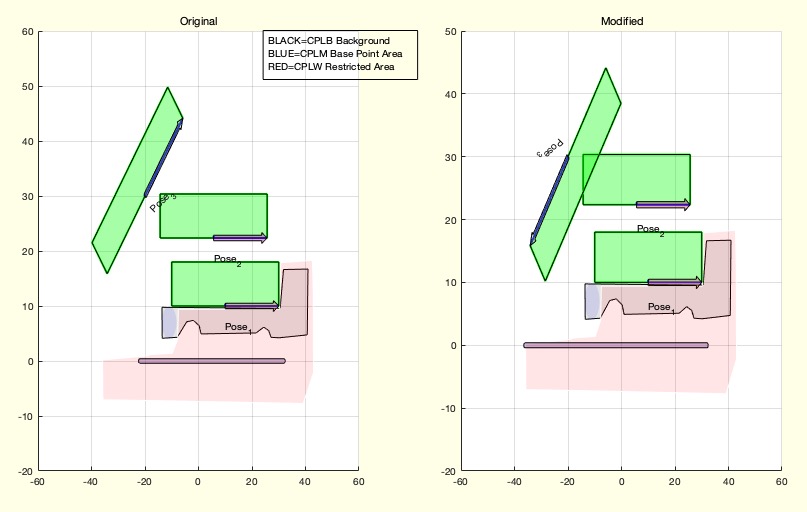
This function just flips the direction of a pose: Start and end points A and B
Poseflip = just flips A and B
PosetransT = just transforms A and B
See Also: PosetransT
, PosetransrelCPLE
Example Illustration
Syntax
PS=Poseflip(PS,[nn])
Input Parameter
PS: | | Pose struct with A and B fields to describe Poses |
nn: | | list of poses to flip; default is all |
Output Parameter
PS: | | Pose with fliped direction |
Examples
Posesample(17);PS=ans;
Poseflip(PS,3) % Be aware what happend with the Contour of the Eeffector CPLE
Copyright 2023-2025 Tim C. Lueth. All rights reserved. The code is the property of Tim C. Lueth and may not be redistributed or modified without explicit written permission. This software may be used free of charge for academic research and teaching purposes only. Commercial use, redistribution, modification, or reverse engineering is strictly prohibited. Access to source code is restricted and granted only under specific agreements. For licensing inquiries or commercial use, please contact: Tim C. Lueth
Algorithm (Workflow)
This algorithm is designed to flip the direction of pose vectors in a given Pose struct. It is part of the SolidGeometry library and is used in kinematics and frames.
Input Parameters
- PS: A Pose struct containing fields A and B, which describe the poses.
- nn: An optional list of poses to flip. If not provided, the default is to flip all poses.
Output
- PS: The Pose struct with the direction of specified poses flipped.
Algorithm Steps
- Store the original Pose struct in
PSO for later comparison.
- Determine which poses to flip using the
getfuncparams function. If nn is not provided, default to flipping all poses by using the size of PS.A.
- Iterate over each pose index in
nn:
- Calculate the vector
ei as the difference between PS.B(i,:) and PS.A(i,:).
- Update
PS.B(i,:) to be PS.A(i,:) minus ei, effectively flipping the direction of the pose vector.
- If no output is requested (
nargout==0), visualize the original and modified poses:
- Create a new figure using
SGfigure.
- In the first subplot, plot the original poses using
Poseplotspace and Poseplot, with a subtitle 'Original'.
- In the second subplot, plot the modified poses with a subtitle 'Modified'.
- Ensure both plots have grid lines and equal axis scaling for comparison.
Algorithm explaination created using ChatGPT on 2025-08-19 00:28. (Please note: No guarantee for the correctness of this explanation)
Last html export of this page out of FM database by TL: 2025-09-21